Η παράλογη αποτελεσματικότητα των Μαθηματικών

« από πού προέρχεται η σοφία, και πού o τόπος της κατανόησης; » Ιωβ. 28.20
Ένα βαθιά κατανοητό σύμπαν
Παίρνω αφορμή για την σύνταξη αυτού του άρθρου το βιβλίο του Ιώβ και συγκεκριμένα τον εικοστό στίχο του εικοστού όγδοου κεφαλαίου,
« ἡ δὲ σοφία πόθεν εὑρέθη; ποῖος δὲ τόπος ἐστὶ τῆς συνέσεως; »
(Που λοιπόν ευρίσκεται η σοφία; Ποίος δε είναι ο τόπος της συνέσεως και της αληθούς γνώσεως;)
Ιώβ. 28.20
…και θα ήθελα να ξεκινήσω θέτοντας μια δεύτερη ερώτηση: γιατί οι άνθρωποι κάνουν έρευνα στην επιστήμη; Είναι σκληρή, μια δουλειά γεμάτη απογοητεύσεις – καθώς οι καλές ιδέες του πρωινού αποδεικνύονται λιγότερο πειστικές στο τελείωμα της ημέρας. Γιατί λοιπόν την κάνουμε;
Η επιτυχία της επιστήμης στην εξερεύνηση του σύμπαντος προέρχεται από το γεγονός ότι το συγκεκριμένο σύμπαν είναι μια δημιουργία προικισμένη με μια τάξη που εμπνέεται από μια εκπληκτική διαφάνεια στην λογικότητα που το διέπει και είναι προσβάσιμο στην κατανόηση της δομής του απο το ανθρώπινο μυαλό. Η σύγχρονη εκπληκτική επιστημονική πρόοδος μας δίνει τη δυνατότητα να μελετούμε το σύμπαν στο σύνολο του. Να διακρίνουμε την αρχή του, να παρακολουθούμε την εξέλιξη του και να συζητούμε για το τέλος του.
Το σύμπαν εκπέμπει ένα λογικό περιεχόμενο και γίνεται αντικείμενο μελέτης από τον άνθρωπο μέσω των επιστημών των οποίων τα Μαθηματικά αποτελούν την κορωνίδα. Τα μαθηματικά είναι η γλώσσα της φύσης. Αυτή όμως η ιδιότητα του κόσμου να είναι κατανοητός είναι ένα από τα μεγαλύτερα μυστήρια. Όπως είπε κάποτε ο Albert Einstein
« Το πιο ακατανόητο πράγμα είναι το ότι ο κόσμος είναι κατανοητός »
Αυτός ο μεγάλος σοφός της επιστήμης θεωρεί εντυπωσιακό και παράδοξο το ότι όλος ό κόσμος έχει δημιουργηθεί έτσι ώστε να ανταποκρίνεται στον βαθύτατο πόθο μας να τον κατανοήσουμε.
Η Μαθηματική ομορφιά του κόσμου
Ο δημιουργημένος κόσμος περιλαμβάνει τα ορατά και αόρατα πράγματα. Ο κόσμος των Μαθηματικών είναι ο κατεξοχήν αόρατος κόσμος, ένας κόσμος που αποτελείται από αριθμητικές και γεωμετρικές δομές, ένας κόσμος λογικής σκέψης. Οι μαθηματικοί πιστεύουν ότι τα θεωρήματα και τα αξιώματά τους ανταποκρίνονται σε μια πραγματικότητα όπως ο κόσμος των ιδεών του Πλάτωνα.
Η σύγχρονη φυσική έρευνα έχει την τάση να επιδιώκει τη συμμετρία. Ακριβώς όπως οι νιφάδες του χιονιού όσο είναι πιο συμμετρικές είναι τόσο πιο όμορφες είναι, έτσι και οι νόμοι της φυσικής θεωρούνται ωραιότεροι όταν εκφράζονται μέσω συμμετρικών εξισώσεων. Μία καλή εξίσωση πρέπει να συμπυκνώνει την αλήθεια με οικουμενικό, απλό και αναπόφευκτο τρόπο. Όπως λέει ο φυσικός του Πανεπιστημίου του Χάρβαρντ Peter Galison
« Στο E=mc² του Αϊνστάιν, οι φιλοδοξίες μας για την επιστήμη, τα όνειρά μας για κατανόηση και οι εφιάλτες μας για καταστροφή συμπυκνώνονται σε μερικά γράμματα »
Είναι αξιοσημείωτο γεγονός στη θεωρητική φυσική ότι οι εξισώσεις που εκφράζουν τους θεμελιώδεις νόμους έχουν μια μαθηματική ομορφιά
« Τα μαθηματικά διαθέτουν όχι μόνο αλήθεια, αλλά και υπέρτατη ομορφιά ψυχρή και αυστηρή, όπως αυτή της γλυπτικής, χωρίς να απευθύνονται σε κανένα μέρος της ασθενέστερης φύσης μας, χωρίς τα πανέμορφα στολίδια της ζωγραφικής ή της μουσικής, αλλά μεγαλειωδώς καθαρά, και ικανά για μια αυστηρή τελειότητα που μόνο η μεγαλύτερη τέχνη μπορεί να επιδείξει. Το αληθινό πνεύμα της απόλαυσης, της ανάτασης, η αίσθηση ότι είσαι κάτι περισσότερο από άνθρωπος, που είναι η λυδία λίθος της υψηλότερης τελειότητας, βρίσκεται στα μαθηματικά με την ίδια βεβαιότητα όπως και στην ποίηση »
Βertrand Russell, Study of Mathematics
Eίναι πράγματι ελάχιστοι οι επιστήμονες που δεν γοητεύονται κάποια στιγμή από την ομορφιά των δικών τους εξισώσεων. Επανηλειμένα έχει βρεθεί ότι μόνο οι εξισώσεις που διαθέτουν την οικονομία και την κομψότητα αυτού του είδους τελικά αποδεικνύεται ότι αποτελούν την βάση για τις θεωρίες. Σύμφωνα με τα λόγια του Paul Dirac είναι πιο σημαντικό για κάποιον να έχουμε μαθηματικές εξισώσεις με ομορφιά από το να ταιριάζουν στο πείραμα.
« Μια θεωρία με μαθηματική ομορφιά είναι πιο πιθανό να είναι σωστή από μια άσχημη θεωρία που ταιριάζει σε κάποια πειραματικά δεδομένα »
Αυτό ήταν και το κριτήριο στην έρευνα του πάνω στην κβαντική θεωρία. Η συνεχής αναζήτηση της ομορφιάς στις εξισώσεις των πειραμάτων του. Εάν η θεωρία δεν συμφωνεί με τις εξισώσεις στις οποίες έχεις καταλήξει πιθανόν τα πειράματα να είναι λάθος ή να έχεις λύσει τις εξισώσεις με λάθος τρόπο. Στην περίπτωση αυτή δεν πρέπει να σε καταβάλλει η απογοήτευση. Υπάρχει κάποια ελπίδα. Αλλά εάν οι εξισώσεις στερούνται ομορφιάς τότε δεν υπάρχει καμμία ελπίδα. Δεν μπορούν να περιγράφουν την πραγματικότητα.
Η παράλογη αποτελεσματικότητα των Μαθηματικών
Όταν χρησιμοποιούμε τα μαθηματικά σαν το κλειδί για να ξεκλειδώσουμε τα μυστικά του σύμπαντος βρισκόμαστε αντιμέτωποι με κάτι πολύ περίεργο. Τα μαθηματικά είναι προΐόντα της αφηρημένης ανθρώπινης σκέψεις αποτελούμενα απο έννοιες, αξιώματα, και θεωρήματα τα οποία χτίζουν ένα συνεπές λογικό σύστημα. Από την άλλη μεριά, οι μαθηματικοί είναι άνθρωποι που επινοούν από το μυαλό τους όλα αυτά τα όμορφα αφηρημένα σύνολα της μαθηματικής λογικής χωρίς πολλές φορές να έχουν γνώση Φυσικής.
Ως παράδειγμα αναφέρω τον K. Gödel ο οποίος υπήρξε ένας απο τις μεγαλύτερες μαθηματικές ιδιοφυίες και ο μεγαλύτερος λογικιστής όλων των εποχών μετά τον Αριστοτέλη. Οι γνώσεις του στην Φυσική ήταν μάλλον περιορισμένες αλλά ήταν αυτός ο οποίος βοήθησε τον Αϊνστάιν στην μαθηματική διατύπωση της θεωρίας της γενικής σχετικότητας παρέχοντας σ’ αυτόν τα κατάλληλα μαθηματικά εργαλεία όπως είναι ο τανυστικός λογισμός (tensor analysis).
Το παράξενο που προκύπτει είναι ότι τα περισσότερα από αυτά τα Μαθηματικά βρίσκουν εφαρμογή με ένα ανεξήγητο τρόπο στην δομή και λειτουργία του φυσικού κόσμου. Αυτά τα όμορφα μοτίβα που οι μαθηματικοί μπορούν να συλλάβουν κατά τη διάρκεια της αφηρημένης λογικής τους σκέψης, αποδεικνύεται ότι βρίσκονται ενσωματωμένα στη δομή του φυσικού κόσμου γύρω τους. Ταιριάζουν απόλυτα σαν γάντι όταν προσπαθούμε να ερμηνεύσουμε τον κόσμο.
Το φθινόπωρο του 1915, ο Αλμπερτ Αϊνστάιν στο Βερολίνο προσπαθούσε να τελειοποιήσει την νέα θεωρία του για τη βαρύτητα, την οποία προηγουμένως είχε επεξεργαστεί μέσα στους λαβυρίνθους της λογικής και των μαθηματικών επί μία δεκαετία. Πριν τελειώσει, έπρεπε να ελέγξει την θεωρία του για τον πλανήτη Ερμή, του οποίου η τροχιά γύρω από τον ήλιο δεν μπορούσε να ερμηνευθεί με βάση την Νευτώνειο μηχανική.

Το σωματίδιο του θεού
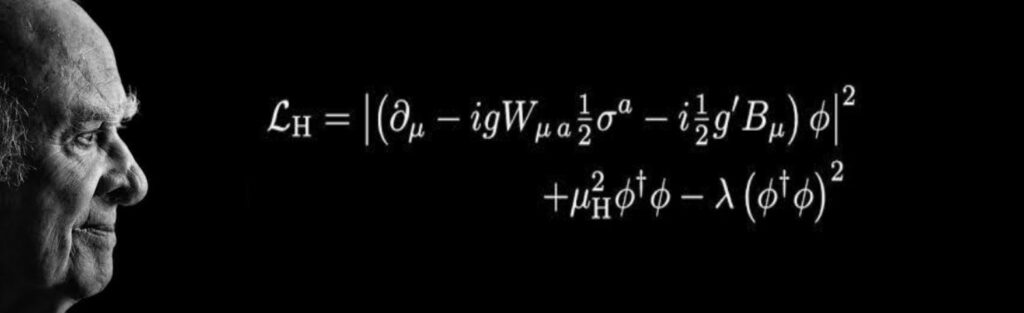
Όταν οι υπολογισμοί με βάση τη νέα θεωρία περιέγραψαν πράγματι την τροχιά του Ερμή οι όποιες αμφιβολίες για τη θεωρία της σχετικότητας μετατράπηκαν σε «άγρια βεβαιότητα». Αργότερα, είπε σ’ ένα μαθητή του ότι αν η θεωρία του είχε διαψευσθεί θα ήταν «πολύ κρίμα για τον Θεό».
Ένας από τους σύγχρονους θεωρητικούς φυσικούς ο John Polkinghorne διερωτάται
« Τι είναι λοιπόν αυτό που δένει τόσο καταπληκτικά την λογική της σκέψης μας (μαθηματικά) με την λογική που είναι δομημένος ο κόσμος; Γιατί είναι ο κόσμος κατανοητός; Γιατί τα μαθηματικά είναι τόσο παράλογα αποτελεσματικά; Τι συνδέει με αυτόν τον αξιοσημείωτο τρόπο την εσωτερική λογική (τη μαθηματική μας σκέψη) και την εξωτερική λογική (την τάξη του νοητού σύμπαντος); »
Πώς είναι δυνατόν, για παράδειγμα, ένας μαθηματικός θεωρητικός όπως Peter Higgs να κάθεται στο γραφείο του και, μελετώντας μαθηματικές εξισώσεις, να προβλέπει την ύπαρξη ενός θεμελιώδους σωματιδίου του σωματιδίου του θεού όπως ονομάστηκε ; Χρειάστηκε ένας αγώνας δρόμου τριάντα χρόνων αργότερα με χιλιάδες εργατοώρες για να ανιχνευθεί μέσω πειραμάτων με πανάκριβους επιταχυντές σωματιδίων. Για τον σκοπό αυτό φτιάχτηκε τελικά και ο Μεγάλος Επιταχυντής Αδρονίων στο CERN στη Γενεύη μια επένδυση εκατομμυρίων δολαρίων.
Αυτό είναι εκείνο το οποίο ο Eugene Wigner ονόμασε ως « the unreasonable effectiveness of mathematics » και στην δημοσίευση του το 1960 έγραψε
« Το θαύμα της καταλληλότητας της γλώσσας των μαθηματικών για τη διατύπωση των νόμων της φυσικής είναι ένα θαυμάσιο δώρο που ούτε καταλαβαίνουμε ούτε αξίζουμε »

Γιατί τα μαθηματικά λοιπόν είναι τόσο παράλογα αποτελεσματικά; Μια αρκετά ικανοποιητική απάντηση είναι αυτή την οποία δίνει ο John Polkingorne.
« Το ερώτημα αυτό μπορεί να απαντηθεί εάν δεχθούμε ότι το σύμπαν δημιουργήθηκε από ένα Νου. Η λογική της σκέψης μας και η λογική από την οποία διέπεται το συμπάν δένουν απόλυτα επειδή έχουν μια κοινή πηγή αυτή της λογικότητας του θεού ο οποίος είναι η βάση της ύπαρξης και της νόησης μας αλλά και της φυσικής μας εμπειρίας μας »
Με άλλα λόγια αυτή η πηγή δεν είναι άλλη από ένα πρόσωπο το πρόσωπο για το οποίο ο Ιωάννης αναφέρει
« Στην αρχή ήταν ο λόγος, κα ο λόγος ήταν παρά το θεό , και θεός ήταν ο λόγος…» Ιωαν. 1.1

Η ικανότητα μας να εξερευνήσουμε επιστημονικά την λογική ομορφιά του σύμπαντος φαίνεται να είναι μέρος του κατ’ εικόνα δώρου του Πατέρα στην ανθρωπότητα, και η όμορφη λογική τάξη του σύμπαντος είναι το αποτύπωμα του Θείου Λόγου. Τα μαθηματικά είναι πράγματι η γλώσσα της φυσικής, είναι όμως ταυτόχρονα και η γλώσσα του Θεού. Αυτός ο κόσμος της λογικής σκέψης πηγάζει και συντηρείται από τον Λόγο. Θεός δημιούργησε όλα τα πράγματα δια μέσου του Λόγου.
« όταν θέσπιζε κύκλο υπεράνω του προσώπου της αβύσσου »
Παροιμ. 8.27
Θεωρούμε λοιπόν ότι ο Λόγος δεν έπλασε απλώς κάποτε στο παρελθόν το σύμπαν και το παράτησε, όπως λέει ο Επίκουρος, αλλά συνεχίζει να ενεργεί σε αυτό. Η παρουσία Του είναι αυτή που συντηρεί την ζωή και την ύπαρξη των δημιουργημάτων απο την απειλή του χάους. Είναι αυτός που δίνει την υπόσταση στο σύμπαν κάθε στιγμή, « υφαίνοντάς το » σε κάθε σημείο του χωροχρόνου, μέσα σε έναν “αφρό κενού”, αποτελούμενο από δυνάμει σωματίδια που στη σύγχρονη φυσική ονομάζουμε κβαντικό κενό.
Παραπομπές
1. The Unreasonable Effectiveness of Mathematics
Communications in Pure and Applied Mathematics, vol. 13, No. I (Febr 1960)

Ο Eugene Paul Wigner (1902 – 1995) ήταν Αμερικανός θεωρητικός φυσικός και μαθηματικός ουγγρικής καταγωγής. Βραβείο Νόμπελ Φυσικής του 1963 «για τη συμβολή του στη θεωρία του ατομικού πυρήνα και των στοιχειωδών σωματιδίων, ειδικότερα μέσω της ανακάλυψης και εφαρμογής θεμελιωδών αρχών συμμετρίας». Έθεσε τα θεμέλια της θεωρίας των συμμετριών στην κβαντομηχανική και ερεύνησε τη δομή του ατομικού πυρήνα. Η σημαντική η συνεισφορά του στα καθαρά μαθηματικά, με τη διατύπωση αρκετών θεωρημάτων. Ιδιαίτερα το «Θεώρημα του Γουίγκνερ» αποτελεί έναν από τους ακρογωνιαίους λίθους της μαθηματικής θεμελιώσεως της κβαντομηχανικής.

Ο Paul Adrien Maurice Dirac (1902 – 1984) ήταν Άγγλος θεωρητικός φυσικός που θεωρείται ένας από τους θεμελιωτές της κβαντικής μηχανικής και της κβαντικής ηλεκτροδυναμικής. Υπήρξε καθηγητής Μαθηματικών Lucasian στο Πανεπιστήμιο του Cambridge, καθηγητής φυσικής στο Πολιτειακό Πανεπιστήμιο της Φλόριντα και στο Πανεπιστήμιο του Μαϊάμι και κάτοχος του Νόμπελ Φυσικής του 1933.

Ο John Polkinghorn (1930 – 2021) διακρίθηκε στην επιστημονική κοινότητα για την επιτυχημένη σταδιοδρομία του ως φυσικός στοιχειωδών σωματιδίων. Eπίσης καταξιώθηκε ως συγγραφέας βιβλίων στα οποία αναλύει τις σχέσεις μεταξύ επιστήμης και θρησκείας. Tο 1974 εκλέχτηκε Mέλος της Bασιλικής Eταιρείας, ενώ από το 1968 ως το 1979 διατέλεσε καθηγητής της Mαθηματικής Φυσικής στο Πανεπιστήμιο του Kέμπριτζ. Tο 1982 χειροτονήθηκε ιερέας της Aγγλικανικής Eκκλησίας. Aπό το 1989, είναι πρόεδρος του Kολεγίου της Bασίλισσας (Queen’s College) στο Kέμπριτζ.

Ο Peter Ware Higgs είναι Άγγλος θεωρητικός φυσικός, ομότιμος καθηγητής στο Πανεπιστήμιο του Εδιμβούργου και κάτοχος του βραβείου Νόμπελ το 2013 για το έργο του σχετικά με τη μάζα των υποατομικών σωματιδίων. Ο Peter Higgs γεννήθηκε στο Newcastle upon Tyne του Ηνωμένου Βασιλείου το 1929. Ελαβε το διδακτορικό του από το King’s College το 1954. Στη συνέχεια μετακόμισε στο Πανεπιστήμιο του Εδιμβούργου, όπου παρέμεινε, με εξαίρεση μερικά χρόνια που πέρασε στο Λονδίνο στα τέλη της δεκαετίας του 1950.
